2024-07-27

個人的に AtCoder で利用しているツール

ツール

個人的に AtCoder で利用している非公式ツールを紹介します。

AtCoder 用のツールは Greasy Fork の拡張機能 (スクリプト) として開発されたものが多いです。これを利用するためにまず、Google Chrome の拡張機能である Tampermonkey をインストールしておきます。

chromewebstore.google.com

コンテスト外でも使うツール

主にコンテスト中に使うツール

参考情報

Scripts - AtCoder Clans

2024-03-15

セグメント木の定義域を拡張する (2)

データ構造

前回の記事では方法 1 について記述しました。
今回はそれを発展させた方法 2 について記述します。

方針

方法 2 では、方法 1 の状態からさらに、子ノードが 1 個のノードを省略します。
下図は、クエリ (1) によりインデックス $2,4,5,6$ の値が更新されたときの例です。
根は $[0,8)$ となります。

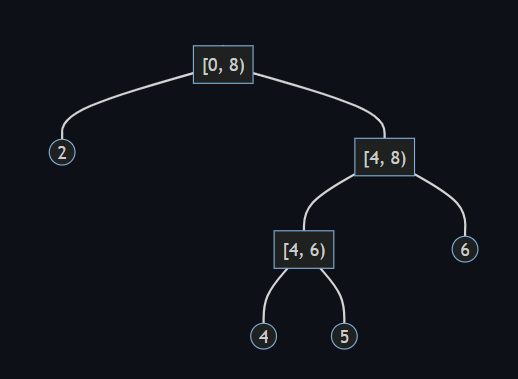
保持するノードを省略することで、メモリ使用量を削減します。
方法 1 とは大きく異なるのが、クエリ (1) において二分木にノードを追加するときの処理です。

例として、クエリ (1) によりまず葉 $2,4,5$ が追加されており、その次に葉 $6$ が追加される場合を考えましょう。
葉 $6$ が追加される前の状態は下図のようになっています。

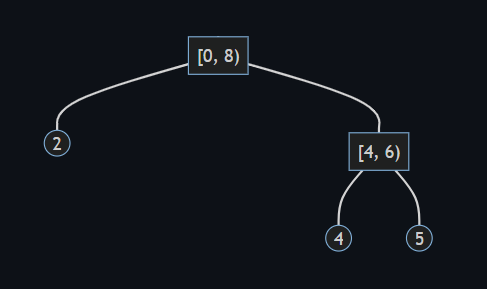
根を出発して葉 $6$ を探索していきます。
$6$ を含まない区間 $[4,6)$ が見つかると、葉 $6$ とノード $[4,6)$ の (元の完全二分木における) 最小共通祖先 (lowest common ancestor; LCA) であるノード $[4,8)$ を挿入し、ノード $[4,6)$ と葉 $6$ をそれぞれ左右の子ノードに設定します。
この方法であれば、1 回のクエリ (1) において新たに追加されるノードはたかだか 2 個であることが保証されます。

これを一般化して、 $i \notin [L, R)$ を満たす葉 $i$ とノード $[L, R)$ の (元の完全二分木における) LCA を求めるには、次のようにビット演算を用います。
なお、& は AND、| は OR、^ は XOR、~ は補数の演算子をそれぞれ表します。

LCA を求める方法
L ^ i の最上位ビットのみを抜き出したものを f とする。
これは、LCA が表す範囲の長さの半分となる。
l := i & ~(f | (f - 1)) とすれば、LCA が表す範囲は $[l, l + 2f)$ となる。

整数に対して最上位ビットのみを抜き出すことは、次のようなビット演算でできます。

static int MaxBit(int x)
{
    x |= x >> 1;
    x |= x >> 2;
    x |= x >> 4;
    x |= x >> 8;
    x |= x >> 16;
    return x ^ (x >> 1);
}

.NET では、BitOperations.LeadingZeroCount メソッドからも求めることができます。

問題集およびソースコード

上記の方法を利用できる問題およびコードを示します。言語は C# です。

ABC 221 E では Range Sum Query (RSQ) に特化したコードを使うことができます。
加算はモノイドの中でも性質がよいため、RSQ のコードを簡略化できます。

1 回のクエリ (1) において新たに追加されるノードはたかだか 2 個であることから、配列ベースの実装においては、クエリが $q$ 回実行される場合、サイズ $O(q)$ の配列を初期化すれば十分です。

まとめ

以上でセグメント木の定義域を拡張し、座標圧縮をせずにオンラインクエリの処理が可能になりました。

さて、二分探索木においてもこれに近い実装が可能で、平衡二分探索木にあるような回転が不要になります。これについてはまた後日投稿します。

作成したサンプル

AlgorithmSample (GitHub)

検証したバージョン

開発環境: C# 10, .NET 6
実行環境: C# 11, .NET 7 (AtCoder)

参照

履歴

2024.03.28 問題集に PAST 13 L を追加

2024-03-12

セグメント木の定義域を拡張する (1)

データ構造

概要

通常のセグメント木では、管理対象の列の項数 $n$ を固定して完全二分木を構築するため、初期化に時間計算量および空間計算量 $O(n)$ を要し、1 回のクエリあたり時間計算量 $O( \log n)$ を要する。したがって、 $n$ として利用できる値には計算機資源上の制限があり、列のインデックス (セグメント木の定義域) としてより大きな値を利用するには、オフラインクエリ (入力値がすべて予め与えられる) を前提として座標圧縮をする必要があった。

そこで本稿では、セグメント木の定義域を拡張し、例えば $[0, 2^{30})$ や $[0, 2^{62})$ のような範囲を利用できる方法について記述する。これにより、座標圧縮をせずにセグメント木のオンラインクエリ (入力値が逐次的に与えられる) を処理することができる。
次の 2 つの方法がある：

方法 1 : 完全二分木のノードのうち、各更新クエリで指定されたインデックスに対応する葉と、根を結ぶパス上のノードのみ保持する。
方法 2 : 方法 1 によるノードのうち、子ノードの個数が 1 のノードを保持しない。

導入

まず準備として、空間 $V$ に対し、二項演算 $*: V \times V \to V$ と単位元 $e$ のペアで特徴付けられるモノイドがあるとします。空間 $V$ の値としては実数、行列などが該当し、二項演算 $*$ としては加算、乗算、 $\max$ などが該当します。また、二項演算 $*$ の時間計算量は $O(1)$ であると仮定しておきます。

セグメント木は通常、項数 $n$ の列に対して区間の集計値を動的に求められるデータ構造である、と説明されると思います。厳密に書くと、次のような操作ができるデータ構造です：

$k$ を非負の整数とする。
項数 $n = 2^{k}$ の列 $(a_i \in V)_{0 \le i \lt n}$ およびモノイド $(*, e)$ に対し、初期値を $a_i = e \ (0 \le i \lt n)$ としたうえで、以下のクエリが任意に実行される。

(1) $a_i$ の値を更新する $(0 \le i \lt n)$
(2) $a_l * \cdots * a_{r-1}$ の値を取得する $(0 \le l \lt r \le n)$

初期化に時間計算量および空間計算量 $O(n)$ を要し、1 回のクエリあたり時間計算量 $O( \log n)$ を要する。

ここで初期化に要する時間計算量および空間計算量を $O(1)$ に改善する方法を考えていきます。
このページではまず、方法 1 について記述します。

方針

通常のセグメント木は、列の項数 $n$ を固定して、完全二分木を構築して初期化します。
下図は $n=8$ の例です。

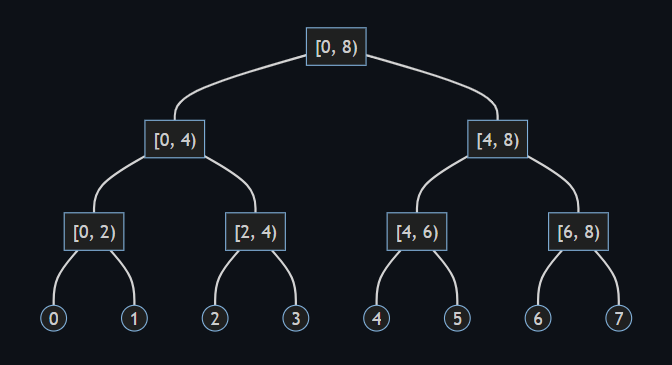
方法 1 では、根は例えば $[0, 2^{30})$ を表すこととし、更新クエリ (1) が実行されたときのみ、指定されたインデックスに対応する葉ノードを追加します。このとき、完全二分木における根と葉を結ぶパス上のノードをすべて追加します。
初期状態ではノードを持ちません。

下図は、クエリ (1) によりインデックス $2,4,5,6$ の値が更新されたときの例です。

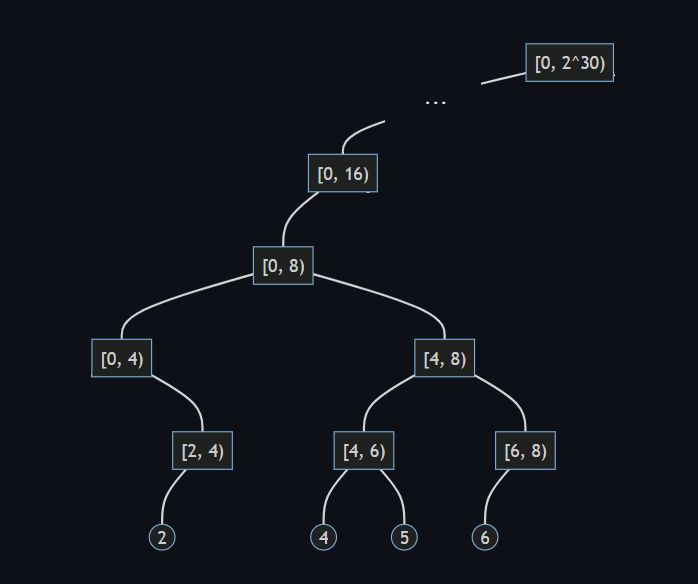
クエリ (1) が実行されていないインデックス $i$ については $a_i = e$ のままです。したがって、各ノードにおいて二項演算 $*$ により集計する際、左または右の子ノードが存在しない場合は、暗黙的に単位元 $e$ が設定されていると見なせばよいです。

以上の方針をノードベース (ノードをオブジェクトで表現する) で実装すれば、初期化に要する時間計算量および空間計算量は $O(1)$ で済みます。
なお、配列ベースで実装することも可能で、クエリが $q$ 回実行される場合は、サイズ $O(q \log n)$ の配列を初期化すればよいです。

問題集およびソースコード

上記の方法を利用できる問題およびコードを示します。言語は C# です。
これらのソースコードでは、定義域を $[-2^{30}, 2^{30})$ としています。

ABC 221 E では Range Sum Query (RSQ) に特化したコードを使うことができます。
加算はモノイドの中でも性質がよいため、RSQ のコードを簡略化できます。

次回は、方法 2 について記述します。

次回: セグメント木の定義域を拡張する (2)

作成したサンプル

AlgorithmSample (GitHub)

検証したバージョン

開発環境: C# 10, .NET 6
実行環境: C# 11, .NET 7 (AtCoder)

参照

Mermaid (グラフの作図)
セグメント木の定義域を拡張する (2)

履歴

2024.03.28 問題集に PAST 13 L を追加

2022-03-20

重み平衡二分木による List, Set, Map

データ構造ライブラリ

重み平衡二分木 (weight-balanced binary trees) を C# で実装したライブラリ WBTrees (GitHub) の初版 v1.0 をリリースしました。

主な機能は次の通りです：
(1) インデックスによる操作 (取得・更新・挿入・削除) をすべて $O( \log n)$ 時間でできる List

WBList<T> クラス
使い方は通常の List<T> に近い

(2) インデックスによる操作 (取得・削除) もすべて $O( \log n)$ 時間でできる Set, Map

WBSet<T>, WBMultiSet<T>, WBMap<TKey, TValue>, WBMultiMap<TKey, TValue> クラス
通常の平衡二分探索木に、インデックスによるアクセス機能を追加したもの
- Weight-balanced tree - Wikipedia
二分探索により、要素からインデックスの取得もできる
安定ソート
WBMultiSet<T> および WBMultiMap<TKey, TValue> はキーの重複を許可する。したがって、両端優先度付きキュー、または安定ソートの優先度付きキューとしても使える

アルゴリズムについて

(1) の List と (2) の Set, Map はともに、内部構造としては重み平衡二分木 (weight-balanced binary trees) です。ここでいう「重み」とは、部分木に含まれるノードの個数 (サイズ) を指し、この実装における Node<T> クラスの Count プロパティに相当します。高さ平衡 (height-balanced) の二分探索木である AVL 木に対し、重みを利用することで自己平衡 (self-balancing) と「インデックスによる二分探索」の両方を実現します。

なお、Wikipedia の Weight-balanced tree によると「weight-balanced binary trees」という用語は平衡二分探索木 (self-balancing binary search trees) の一種として定義されています。一般に、二分探索木という場合にはソート済みの制約が付けられた二分木を指し、この制約により「要素による二分探索」が可能となります。上の Wikipedia の記事もその制約を前提として書かれているようですが、実際にはソート済みではなく「要素による二分探索」が可能でない実装もあり得る、というのが本ライブラリの主張です。

そこで、ここでは単に、重み平衡二分木 (weight-balanced binary trees) は、重みによる自己平衡機構を持つ「二分木」であると定義します。すると、このデータ構造は「インデックスによる二分探索」が $O( \log n)$ 時間でできるという性質を持ちます。このうち「要素による二分探索」の機能を持たないものが (1) の List、持つものが (2) の Set, Map です。

さらに、自己平衡機構と「インデックスによる二分探索」の議論は分解できます。
すなわち、サイズ付き二分木 (sized binary trees) は、各ノードが重み (サイズ) を保持する二分木であると定義します。するとこのデータ構造は、高さが $h$ のとき「インデックスによる二分探索」が $O( h)$ 時間でできるという性質を持ちます。これが何らかの自己平衡機構を持てば $O( \log n)$ 時間となることが保証されます。したがって、AVL 木や赤黒木 (二色木) など、従来の平衡二分木の構造をベースにしたリストの存在も考えられます (ただし多くの場合、各ノードが保持する情報量は増えるでしょう)。実際、AVL 木によるリストについては動作確認済みです。

次の表は System.Collections.Generic.List<T> と WBList<T> の時間計算量の比較です：

操作	`List<T>`	`WBList<T>`
Get by Index	`O(1)`	`O(log n)`
Set by Index	`O(1)`	`O(log n)`
Remove by Index	`O(n)`	`O(log n)`
Insert by Index	`O(n)`	`O(log n)`
Prepend	`O(n)`	`O(log n)`
Add	`O(1)`	`O(log n)`
Get All	`O(n)`	`O(n)`

次の表は System.Collections.Generic.SortedSet<T> と WBSet<T> の時間計算量の比較です：

操作	`SortedSet<T>`	`WBSet<T>`
Get by Item	`O(log n)`	`O(log n)`
Remove by Item	`O(log n)`	`O(log n)`
Add	`O(log n)`	`O(log n)`
Get by Index	`O(n)`	`O(log n)`
Remove by Index	`O(n)`	`O(log n)`
Get Index by Item	`O(n)`	`O(log n)`
Get All	`O(n)`	`O(n)`

List に対する Add は「末尾に追加する」を意味し、Set に対する Add は「順序を保つように追加する」を意味することに注意してください。

バージョン情報

パッケージ

WBTrees は .NET プラットフォーム向けにビルドされ、NuGet Gallery にパッケージが発行されています。ターゲットフレームワークは次のように設定されています：

.NET 5
.NET Standard 2.0

これら以降のバージョンがサポートされます。
.NET Standard 2.0 は .NET Core 2.0 や .NET Framework 4.6.1 などの多くの環境を含んでいます。詳細は .NET Standard で確認できます。

(競技プログラミング向け)
競技プログラミングでは NuGet を使えないため、ソースコードを単一のファイルにまとめたものを downloads で入手してください。

プログラミング言語

WBTrees のソースコードは C# 7.3 で書かれています。これは .NET Standard 2.0 に対応する C# のバージョンであるためです。ただし、AOJ の環境である Mono 6.10 で動作させるために、一部の機能を使っていません。
他の言語への移植も歓迎します。

使用例

このライブラリの使い方は Usage (Wiki) に書かれています (まだ完全に網羅できていませんが)。以下では、そのうち特徴的なものを挙げていきます。

まず、WBTrees 名前空間の using ディレクティブを追加します。

using System;
using System.Collections.Generic;
using System.Linq;
using WBTrees;

(1) List

WBList<T> の基本的な使い方は通常の List<T> に近いです。挿入または削除が $O( \log n)$ 時間で済むことによる利点が生きる場面で使うとよいでしょう。

var list = new WBList<int>();

// データを渡して初期化するには、コンストラクターではなく Initialize を呼び出します。
list.Initialize(Enumerable.Range(0, 100));

list.Prepend(123); // 先頭に追加
list.Add(-234);
list.Insert(3, 345);
list.RemoveAt(5);

var item = list[7];
list[9] = 456;

// 半開区間 [left, right) における要素を列挙します。
var items = list.GetItems(20, 30).ToArray();

(2) Set, Map

WBSet<T> の基本的な使い方は SortedSet<T> に近いです。
同様に、WBMap<T> の基本的な使い方は SortedDictionary<T> に近いです。

要素による二分探索でノードを取得するには、条件を指定して GetFirst または GetLast メソッドを呼び出します。例えば GetFirst であれば「指定された条件を満たす最初のノード」を取得することができます：

var set = new WBSet<int> { 4, 1, 5, 9, 2 }; // 1, 2, 4, 5, 9

// 以上・超・以下・未満の違いを不等号で指定できます。
var f1 = set.GetFirst(x => x >= 2).Item; // 2
var f2 = set.GetFirst(x => x > 2).Item;  // 4
var l1 = set.GetLast(x => x <= 2).Item;  // 2
var l2 = set.GetLast(x => x < 2).Item;   // 1

var f3 = set.GetFirst(x => x > 9); // null
var l3 = set.GetLast(x => x < 1);  // null

Remove*** メソッドも Get*** メソッドと同様に、Node<T> オブジェクトを返します。 null は、指定された条件を満たす要素が存在しないことを意味します。

同様にして、要素による二分探索でインデックスを取得できます。例えば GetLastIndex であれば「指定された条件を満たす最後のインデックス」を取得することができます：

var set = new WBSet<int> { 4, 1, 5, 9, 2 }; // 1, 2, 4, 5, 9

var fi1 = set.GetFirstIndex(x => x > 2); // 2
var li1 = set.GetLastIndex(x => x < 2);  // 0

var fi2 = set.GetFirstIndex(x => x > 9); // 5 (set.Count)
var li2 = set.GetLastIndex(x => x < 1);  // -1

インデックスを指定してノードを取得または削除するには、GetAt または RemoveAt メソッドを呼び出します：

var set = new WBMultiSet<int> { 3, 1, 4, 1, 5, 9, 2, 6, 5 }; // 1, 1, 2, 3, 4, 5, 5, 6, 9

var item = set.GetAt(6).Item; // 5
var node = set.GetAt(-2); // null
var removedItem = set.RemoveAt(8).Item; // 9

// 半開区間 [left, right) における要素を列挙します。
var items = set.GetItems(1, 4).ToArray(); // 1, 2, 3

また、Node<T> および Node<KeyValuePair<TKey, TValue>> に対しては拡張メソッドを用意しています：

var map = new WBMap<int, int>
{
    { 3, 1 },
    { 4, 1 },
    { 5, 9 },
    { 2, 6 },
};

var value5 = map[5]; // 9
var value6 = map.Get(6).GetValueOrDefault(-1); // -1

// priority queue
while (map.RemoveFirst().TryGetValue(out var value))
{
}

問題集

List が使える競技プログラミングの問題：

Set, Map が使える競技プログラミングの問題：

参照

履歴

2022.03.22 その他の平衡二分木によるリストの実現可能性について追記
2022.05.17 重み付き (weighted) をサイズ付き (sized) に変更

2021-07-26

第6回アルゴリズム実技検定 M 解説

問題解説アルゴリズム実技検定

第6回アルゴリズム実技検定 (PAST) の問題 M - 等しい数の解説です。
この記事では、範囲更新クエリ (RUQ) または平衡二分探索木を利用した解法を紹介します。
問題文はリンク先を参照してください。 atcoder.jp

解法の全体構成

まず、解法の全体構成は次のようになります。

同じ値が連続している部分を1つの区間と考える。クエリによる値の変更を何らかのデータ構造で管理することにより、各クエリに対して「どの値が何個増えたか (減ったか)」を求める。なお、1回のクエリにより、複数の値 (区間) が影響を受ける可能性がある。
それぞれの値 (区間) に対する差分を全体の組合せ数に反映させる。

後半の 2. のほうは、ある値の個数を $c$ としたときの組合せ数が ${}_c C_2 = \frac{1}{2} c(c-1)$ であることから、各値に対する増減量が与えられれば、差分を逐次計算することで出力する値を $O(1)$ で調整できます。

さて、1. については、各クエリに対し、関連する区間を削除および追加することを考えます。両端においても、区間が少しでも重なっていれば操作の対象とします。
これにより 2. がサブルーチンとして実行される回数を考えると、初期状態から存在する区間のうち削除されるものはたかだか $N$ 個で、1回のクエリにより追加される区間はたかだか $3$ 個であることから、全体では $O(N+Q)$ であることに気付いておく必要があります。

RUQ の利用

「同じ値が連続する区間のデータをどのように管理するか」がこの問題の難しい部分だと思います。ここでは、範囲更新クエリ (Range Update Query; RUQ) を利用することを考えます。

RUQ は、1回のクエリで、数列の区間 (連続する複数のインデックス) に対して同一の値を設定することを指します。具体的にはセグメント木 (Segment Tree) で実装すればよいです。
参照: Range Update Query (AOJ)

この問題では、任意のインデックスに対して、それが属する区間の情報を取得できればよさそう、というのがポイントです。区間の情報というのは「左端と右端のインデックス」でも「左端のインデックスと長さ」でもよいです。

解法として、次の2通りを考えました。

(1) RUQ で、各インデックスが属する区間の情報を保持する。すなわち、ある区間が半開区間 $[L, R)$ で表せるとき、それに含まれる全てのインデックスに対して、値のペア $(L, R)$ を設定する。提出コード (C#)

(2) 大きな方針は (1) と同様で、「各インデックスが属する区間の左端のインデックスを保持する RUQ」と「左端のインデックスをキーとして、右端のインデックス (開区間) を保持する配列」を用意する。提出コード (C#)

実装は (1) のほうが少しシンプルだと思いますが、隣の区間の情報を探索するために毎回 RUQ を呼び出すことになり、定数倍が重くなります。 (2) であれば、隣の区間はすぐに得られます。

いずれの解法においても、RUQ をセグメント木により実装することで、時間計算量 $O((N+Q) \log N)$ で実行できます。

平衡二分探索木の利用

上記と同様の考え方により、平衡二分探索木を利用して解くこともできます。 1つの区間を1つの要素として格納すればよいため、発想としてはこちらのほうが自然かもしれません。

なお、今回の問題を解くためには、複数の区間についての探索ができる平衡二分探索木である必要があります。
参照: Set: Range Search (AOJ)
参照: Map: Range Search (AOJ)

解法として、次の2通りを考えました。

(1) 順序付き集合 (set) を表す平衡二分探索木で、各区間の情報を保持する。提出コード (C#)

(2) 順序付き連想配列 (map) を表す平衡二分探索木で、各区間の情報を保持する。すなわち、左端のインデックスをキーとして、右端のインデックス (開区間) を値として保持する。提出コード (C#)

いずれの解法においても、時間計算量 $O((N+Q) \log N)$ で実行できます。

まとめ

通常の RUQ であれば、数列の値 $A_i$ をそのまま保持させることを考えるでしょう。しかし今回のように、区間に関する別の情報を保持することで応用範囲が広がることがあります。

補記

平方分割で実装してみるとどうしても不正解になってしまったため、別解を考えた結果です。

2020-12-12

ハイパー LINQ 集 (AtCoder 2020年4月)

ハイパー LINQ 集

// Competitive Programming (1) Advent Calendar 2020 および C# その2 Advent Calendar 2020 の 12 日目の記事です。

このシリーズでは、C#、とくに LINQ で簡潔に書ける競技プログラミングの問題を集めて記事にしています。 Advent Calendar ということで、本来ならこの時点で AtCoder の2020年11月分を書くつもりでしたが、まったく追いつかなくなってしまいました。というわけで、2020年4月分の記事です。

2020年4月といえば、Judge System Update Test Contest 202004 で言語アップデートが実施され、定期開催コンテストとしては ABC 162 から C# 8.0 (.NET Core 3.1.201 など) で提出できるようになりました。

ところで、毎月分を一つの記事としているのですが、ここ数か月間の AtCoder の出題傾向を見ると、LINQ で瞬時に書けるような素直なデータ集計問題は減ってきています。
~~たぶん乱獲のせいです。~~
C# の短いコードでも茶色・緑色近辺で十分戦えるという趣旨で書いてきたのですが、このシリーズが今後どうなるかはわかりません。

さて、以下は本題で、前回までと同様の体裁です。

2020年4月の AtCoder の問題を、LINQ (C#) を使って解いていきます。全8問。
今回は第2回アルゴリズム実技検定も対象としています。
問題文はそれぞれのリンク先を参照してください。

■ ABC 161 B - Popular Vote

投票数の和 $S$ を求めておき、 $A_i$ のうち $\dfrac{S}{4M}$ 以上となるものの個数が $M$ 以上であるかどうかを判定します。
なお、小数を使うと誤差を考慮しなければならなくなるため、整数型のまま比較します。

using System;
using System.Linq;

class B
{
    static int[] Read() => Console.ReadLine().Split().Select(int.Parse).ToArray();
    static void Main()
    {
        var m = Read()[1];
        var a = Read();

        var s = a.Sum();
        Console.WriteLine(a.Count(x => 4 * m * x >= s) >= m ? "Yes" : "No");
    }
}

■ ABC 161 D - Lunlun Number

LINQ で書くのは若干気が引ける問題でも LINQ を使い込み切りましょう。
実行速度が犠牲になるコードとなっていますが、これくらいなら気にしません。

まず、i 桁のルンルン数リストから i + 1 桁のルンルン数リストを生成するためのローカル関数 Next を用意しておきます。ここでは i 桁の各ルンルン数に対し、その下1桁との差の絶対値が1以下の数字 (10種類のうちたかだか3種類) をその末尾に追加することで、i + 1 桁の新たなルンルン数を作ります。

あとはジャグ配列を用意して、各桁のルンルン数リストを順次格納していき、それらの要素をすべて列挙して K 番目を求めます。
なお、問題文の出力例 4 を見れば、制約により最大10桁で収まることがわかります。

using System;
using System.Linq;

class D
{
    static void Main()
    {
        var k = int.Parse(Console.ReadLine()) - 1;

        long[] Next(long[] a) => a.SelectMany(x => Enumerable.Range(0, 10).Where(d => Math.Abs(x % 10 - d) <= 1).Select(d => x * 10 + d)).ToArray();

        var lun = new long[10][];
        lun[0] = Enumerable.Range(1, 9).Select(i => (long)i).ToArray();
        Console.WriteLine(Enumerable.Range(0, 10).SelectMany(i => i > 0 ? lun[i] = Next(lun[i - 1]) : lun[i]).ElementAt(k));
    }
}

■ Judge System Update Test Contest 202004 B - Picking Balls

第1キーをボールの色 ("R", "B" の順)、第2キーをボールに書かれた数値としてソートし、ボールに書かれた数値を出力します。

なお、タプル型を使うと、複数キーによるソートが OrderBy だけで (ThenBy を使わずに) できます。ここでは (bool, int) 型としています。 bool 型では false, true が昇順です。

using System;
using System.Linq;

class B
{
    static void Main()
    {
        var n = int.Parse(Console.ReadLine());
        var q = new int[n]
            .Select(_ => Console.ReadLine().Split())
            .Select(x => (x[1] == "B", v: int.Parse(x[0])))
            .OrderBy(x => x)
            .Select(b => b.v);
        Console.WriteLine(string.Join("\n", q));
    }
}

■ ABC 162 B - FizzBuzz Sum

1 から N までの整数のうち、3でも5でも割り切れないものの和を求めます。

using System;
using System.Linq;

class B
{
    static void Main()
    {
        var n = int.Parse(Console.ReadLine());
        Console.WriteLine(Enumerable.Range(1, n).Where(x => x % 3 > 0 && x % 5 > 0).Sum(x => (long)x));
    }
}

■ 第2回アルゴリズム実技検定 B - Plurality Voting

候補者を表す文字をキーとしてグループ化し、その要素数の降順に並べ替えて、先頭のグループのキーを求めます。

using System;
using System.Linq;

class B
{
    static void Main() => Console.WriteLine(Console.ReadLine().GroupBy(x => x).OrderByDescending(g => g.Count()).First().Key);
}

■ ABC 163 B - Homework

遊ぶことができる日数は、 $N$ から $A_i$ の和を引いた値です。
これが負になる場合は、-1 に切り上げます。

using System;
using System.Linq;

class B
{
    static int[] Read() => Console.ReadLine().Split().Select(int.Parse).ToArray();
    static void Main()
    {
        var n = Read()[0];
        var a = Read();
        Console.WriteLine(Math.Max(n - a.Sum(), -1));
    }
}

■ ABC 163 C - management

$A_i$ の値をキーとしてグループ化し、各グループの要素数を出力します。

ToLookup で返される Lookup<TKey, TElement> クラスでは、指定されたキーが存在しない場合でも要素数 0 のコレクションを返します。 Dictionary<TKey,TValue> クラスのようなキーの存在による場合分けは必要ありません。

using System;
using System.Linq;

class C
{
    static void Main()
    {
        var n = int.Parse(Console.ReadLine());
        var d = Console.ReadLine().Split().Select(int.Parse).ToLookup(x => x);
        Console.WriteLine(string.Join("\n", Enumerable.Range(1, n).Select(i => d[i].Count())));
    }
}

■ ABC 164 C - gacha

重複を排除して要素の個数を求めます。

using System;
using System.Linq;

class C
{
    static void Main() => Console.WriteLine(new int[int.Parse(Console.ReadLine())].Select(_ => Console.ReadLine()).Distinct().Count());
}

バージョン

C# 8.0
- .NET Core 3.1.201 で AC 済

競技プログラミングでも C# で簡潔に書きたい | Do Design Space

2020-09-07

ハイパー LINQ 集 (AtCoder 2020年3月)

ハイパー LINQ 集

2020年3月の AtCoder の問題を、LINQ (C#) を使って解いていきます。全11問。
問題文はそれぞれのリンク先を参照してください。

ABC 157 B - Bingo

選ばれた数をハッシュセット HashSet<int> に格納しておきます。
縦 (3種類) ・横 (3種類) ・斜め (2種類) のいずれかについて、
3つの数がすべてハッシュセットに含まれているかどうかを判定します。

using System;
using System.Linq;

class B
{
    static void Main()
    {
        var a = new int[3].Select(_ => Console.ReadLine().Split().Select(int.Parse).ToArray()).ToArray();
        var n = int.Parse(Console.ReadLine());
        var b = new int[n].Select(_ => int.Parse(Console.ReadLine())).ToHashSet();

        var r3 = new[] { 0, 1, 2 };
        Console.WriteLine(r3.Any(j => a.All(ai => b.Contains(ai[j]))) || a.Any(ai => ai.All(b.Contains)) || r3.All(i => b.Contains(a[i][i])) || r3.All(i => b.Contains(a[i][2 - i])) ? "Yes" : "No");
    }
}

ABC 157 C - Guess The Number

0 から 999 までの整数を文字列に変換し、そのうち最初に長さが N で $s_i$ と $c_i$ の条件をすべて満たすものを求めます。それが存在しなければ "-1" とします。

using System;
using System.Linq;

class C
{
    static int[] Read() => Console.ReadLine().Split().Select(int.Parse).ToArray();
    static void Main()
    {
        var h = Read();
        int n = h[0], m = h[1];
        var scs = new int[m].Select(_ => Read()).ToArray();

        var r = Enumerable.Range(0, 1000)
            .Select(i => i.ToString())
            .FirstOrDefault(x => x.Length == n && scs.All(sc => x[sc[0] - 1] - '0' == sc[1]));
        Console.WriteLine(r ?? "-1");
    }
}

ABC 158 A - Station and Bus

出現する文字の種類数が2なのか1なのかを判定します。

using System;
using System.Linq;

class A
{
    static void Main() => Console.WriteLine(Console.ReadLine().Distinct().Count() > 1 ? "Yes" : "No");
}

ABC 158 C - Tax Increase

1 から 1009 までの整数のうち、最初にその 8% が A, 10% が B となるものを求めます。
なお、浮動小数点数型では誤差が生じる可能性があるため、整数型または10進数型を使います。

using System;
using System.Linq;

class C
{
    static void Main()
    {
        var h = Console.ReadLine().Split().Select(int.Parse).ToArray();
        var r = Enumerable.Range(1, 1009).FirstOrDefault(x => x * 8 / 100 == h[0] && x / 10 == h[1]);
        Console.WriteLine(r > 0 ? r : -1);
    }
}

日立製作所社会システム事業部プログラミングコンテスト2020 A - Hitachi String

"hi" を $[|S|/2]$ 回繰り返して結合したものが S に一致するかどうかを判定します。
長さが奇数のときは自動的に不一致となります。

using System;
using System.Linq;

class A
{
    static void Main()
    {
        var s = Console.ReadLine();
        Console.WriteLine(string.Join("", Enumerable.Repeat("hi", s.Length / 2)) == s ? "Yes" : "No");
    }
}

日立製作所社会システム事業部プログラミングコンテスト2020 B - Nice Shopping

「各割引券を使う場合」のほかに「最安の冷蔵庫と最安の電子レンジを買う場合」を追加し、それら M + 1 種類の支払総額の最小値を求めます。

using System;
using System.Linq;

class B
{
    static int[] Read() => Console.ReadLine().Split().Select(int.Parse).ToArray();
    static void Main()
    {
        var h = Read();
        var a = Read();
        var b = Read();
        Console.WriteLine(new int[h[2]].Select(_ => Read()).Select(v => a[v[0] - 1] + b[v[1] - 1] - v[2]).Append(a.Min() + b.Min()).Min());
    }
}

ABC 159 B - String Palindrome

S が回文であり、かつ前方の $[|S|/2]$ 文字と後方の $[|S|/2]$ 文字が一致するかどうかを判定します。

using System;
using System.Linq;

class B
{
    static void Main()
    {
        var s = Console.ReadLine();
        var h = s.Length / 2;
        Console.WriteLine(string.Join("", s.Reverse()) == s && s[..h] == s[^h..] ? "Yes" : "No");
    }
}

ABC 159 D - Banned K

まず、書かれた整数ごとにグループ化し、それぞれの個数を求めて辞書化します。
次に N 個すべてから選び出す方法の数 M を求めておきます。
すると各 k に対して、 $A_k$ の個数が r であったとすると、
N - 1 個から選び出す方法の数は $M- {}_r C_2+ {}_{r-1} C_2$ となります。

using System;
using System.Linq;

class D
{
    static void Main()
    {
        var n = int.Parse(Console.ReadLine());
        var a = Console.ReadLine().Split().Select(int.Parse).ToArray();

        var d = a.GroupBy(x => x).ToDictionary(g => g.Key, g => g.LongCount());
        var M = d.Sum(p => p.Value * (p.Value - 1) / 2);
        Console.WriteLine(string.Join("\n", a.Select(x => M - d[x] + 1)));
    }
}

ABC 160 C - Traveling Salesman around Lake

家の位置情報を N + 1 軒目 (2周目の1軒目) まで延長しておきます。
1周の長さ K から隣同士の家の間隔の最大値を引いた値を求めます。

using System;
using System.Linq;

class C
{
    static void Main()
    {
        var h = Console.ReadLine().Split().Select(int.Parse).ToList();
        int k = h[0], n = h[1];
        var a = Console.ReadLine().Split().Select(int.Parse).ToList();
        a.Add(k + a[0]);
        Console.WriteLine(k - Enumerable.Range(0, n).Max(i => a[i + 1] - a[i]));
    }
}

ABC 160 D - Line++

本来は二重ループを使って解ける問題ですが、LINQ のクエリ式を使ってみます。
整数の組 $(i,j) (i \lt j)$ に対して、X と Y の間の辺を通らない場合と通る場合の距離の最小値を求め、それをキーにして辞書化します。あとは各 k に対してその個数を出力します。

using System;
using System.Linq;

class D
{
    static void Main()
    {
        var h = Console.ReadLine().Split().Select(int.Parse).ToArray();
        int n = h[0], x = h[1], y = h[2];

        var q =
            from i in Enumerable.Range(1, n)
            from j in Enumerable.Range(i + 1, n - i)
            select Math.Min(j - i, Math.Abs(i - x) + 1 + Math.Abs(j - y));
        var d = q.ToLookup(v => v);
        Console.WriteLine(string.Join("\n", Enumerable.Range(1, n - 1).Select(v => d[v].Count())));
    }
}

ABC 160 E - Red and Green Apples

「 $p_i$ の大きい順に先頭から X 個」「 $q_i$ の大きい順に先頭から Y 個」「 $r_i$ のすべて」を結合したもののうち、大きい順に先頭から X + Y 個の和を求めます。

using System;
using System.Linq;

class E
{
    static int[] Read() => Console.ReadLine().Split().Select(int.Parse).ToArray();
    static void Main()
    {
        var h = Read();
        int x = h[0], y = h[1];
        var p = Read();
        var q = Read();
        var r = Read();
        Console.WriteLine(p.OrderByDescending(v => v).Take(x).Concat(q.OrderByDescending(v => v).Take(y)).Concat(r).OrderByDescending(v => v).Take(x + y).Sum(v => (long)v));
    }
}

バージョン

C# 8.0
- .NET Core 3.1.201 で提出
- 現行の AtCoder では、3種類の C# を選べる
- 今回のコードは、ABC 159 B 以外は C# 6 でも可

コンテスト外でも使うツール

主にコンテスト中に使うツール

参考情報

方針

問題集およびソースコード

まとめ

作成したサンプル

検証したバージョン

参照

履歴

概要

導入

方針

問題集およびソースコード

作成したサンプル

検証したバージョン

参照

履歴

アルゴリズムについて

バージョン情報

パッケージ

使用例

(1) List

(2) Set, Map

問題集

参照

履歴

解法の全体構成

RUQ の利用

平衡二分探索木の利用

まとめ

補記

バージョン

関連記事

バージョン